Research
In my research, I use computer simulations to study the phase behavior and dynamics of many-body systems. Broadly, my research interests can be divided up into three main categories: structure and dynamics in glassy materials, the behavior of bond-forming liquids, and the self-assembly of colloidal particles.Below are some past research highlights.
Negative Laplace pressure in hard-sphere crystal nuclei
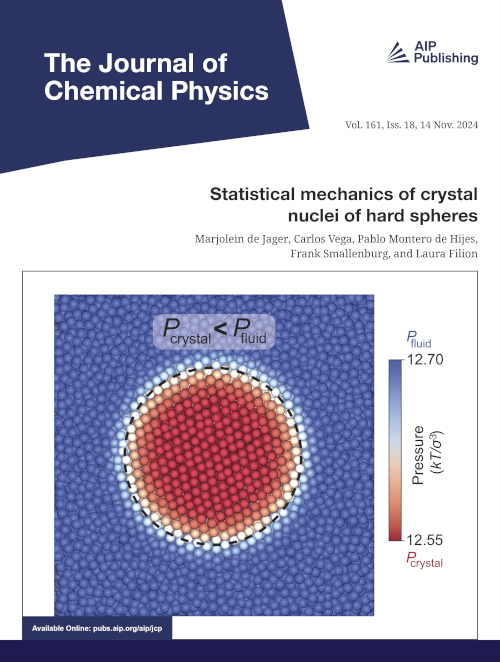 If we look at a droplet of liquid in a gas, the Young-Laplace law tells us that the pressure inside the droplet is higher than on the outside, because the interfacial free energy (i.e. the surface tension) between the liquid and gas tries to minimize the surface area of the gas-liquid interface. Intriguingly, if we instead look at a spherical nucleus of crystal phase inside a fluid, this no longer holds. In contrast to a liquid, crystals can be deformed, changing their lattice spacing with respect to the equilibrium value that would be favored in equilibrium for a large crystal. This provides the nucleus with another way of reducing its surface tension: by adapting the crystal lattice spacing a little bit. As we show in this work, for hard spheres it turns out that increasing the lattice spacing within the crystal can reduce the interfacial free energy. As a result, the surface of a nucleus is stretched out a bit due to its contact with the fluid, resulting in a lower pressure inside the nucleus.
If we look at a droplet of liquid in a gas, the Young-Laplace law tells us that the pressure inside the droplet is higher than on the outside, because the interfacial free energy (i.e. the surface tension) between the liquid and gas tries to minimize the surface area of the gas-liquid interface. Intriguingly, if we instead look at a spherical nucleus of crystal phase inside a fluid, this no longer holds. In contrast to a liquid, crystals can be deformed, changing their lattice spacing with respect to the equilibrium value that would be favored in equilibrium for a large crystal. This provides the nucleus with another way of reducing its surface tension: by adapting the crystal lattice spacing a little bit. As we show in this work, for hard spheres it turns out that increasing the lattice spacing within the crystal can reduce the interfacial free energy. As a result, the surface of a nucleus is stretched out a bit due to its contact with the fluid, resulting in a lower pressure inside the nucleus.
In collaboration with M. de Jager, C. Vega, P. M. de Hijes, and L. Filion.
Link to paper: J. Chem. Phys. arXiv
Fast event-driven simulations for slightly soft spheres
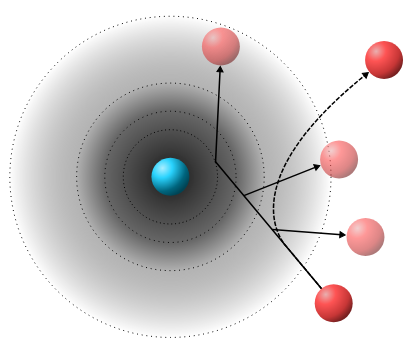 Molecular dynamics simulations function by integrating Newton's equations of motion. Typically, this is done by dividing time up into small, discrete time steps, and repeatedly calculating the forces on each particle, and the resulting changes in velocity, during each step. While extremely powerful, this method can struggle with interaction potentials where the force changes rapidly as a function of distance, such as almost-hard-sphere particles. In that case, very small time steps will be needed to perform accurate simulations, resulting in long simulation times. In this work, we show that for suitable models, this problem can be circumvented by an event-driven Monte Carlo approach, which handles collisions between particles as hard-sphere elastic collisions at a stochastically determined collision distance. For a sharply repulsive model system, this method, originally proposed by Peters and De With, turns out to closely match the dynamics of conventional MD, while running up to ~25 times faster. We use this high efficiency to take a closer look at the low-temperature nucleation behavior of slightly soft spheres into a binary crystal structure.
In collaboration with A. Castagnède and L. Filion.
Molecular dynamics simulations function by integrating Newton's equations of motion. Typically, this is done by dividing time up into small, discrete time steps, and repeatedly calculating the forces on each particle, and the resulting changes in velocity, during each step. While extremely powerful, this method can struggle with interaction potentials where the force changes rapidly as a function of distance, such as almost-hard-sphere particles. In that case, very small time steps will be needed to perform accurate simulations, resulting in long simulation times. In this work, we show that for suitable models, this problem can be circumvented by an event-driven Monte Carlo approach, which handles collisions between particles as hard-sphere elastic collisions at a stochastically determined collision distance. For a sharply repulsive model system, this method, originally proposed by Peters and De With, turns out to closely match the dynamics of conventional MD, while running up to ~25 times faster. We use this high efficiency to take a closer look at the low-temperature nucleation behavior of slightly soft spheres into a binary crystal structure.
In collaboration with A. Castagnède and L. Filion.Link to paper: J. Chem. Phys. arXiv
Quasicrystals of hard spheres on a plane
 Quasicrystals are exotic materials that are highly ordered but lack the periodicity of conventional crystal phases. This allows them to have symmetries that are forbidden to normal crystals. Although quasicrystals were originally discovered in metallic alloys, there are now a handful of soft-matter systems known to form quasicrystals. Recently, we have used computer simulations to discover that two different quasicrystals can form in an extremely simple model system: hard spheres resting on a flat plane. In particular, we use two different sizes of spheres. Depending on the mixture, our simulations show these particles can spontaneously organize themselves into either a dodecagonal or octagonal quasicrystal. Both structures can be interpreted as a random tiling of squares and triangles, which occur in ratios that can be predicted by regarding the quasicrystal as a projection of a four-dimensional periodic lattice. In follow-up studies, we have additionally demonstrated the importance of configurational entropy for the stability of the dodecagonal quasicrystal, and the experimental realization of an octagonal granular quasicrystal based on this work.
Quasicrystals are exotic materials that are highly ordered but lack the periodicity of conventional crystal phases. This allows them to have symmetries that are forbidden to normal crystals. Although quasicrystals were originally discovered in metallic alloys, there are now a handful of soft-matter systems known to form quasicrystals. Recently, we have used computer simulations to discover that two different quasicrystals can form in an extremely simple model system: hard spheres resting on a flat plane. In particular, we use two different sizes of spheres. Depending on the mixture, our simulations show these particles can spontaneously organize themselves into either a dodecagonal or octagonal quasicrystal. Both structures can be interpreted as a random tiling of squares and triangles, which occur in ratios that can be predicted by regarding the quasicrystal as a projection of a four-dimensional periodic lattice. In follow-up studies, we have additionally demonstrated the importance of configurational entropy for the stability of the dodecagonal quasicrystal, and the experimental realization of an octagonal granular quasicrystal based on this work.The image shows the octagonal quasicrystal (top) and its Fourier transform higlighting its eight-fold symmetry (bottom).
In collaboration with E. Fayen, M. Impéror-Clerc, L. Filion, and G. Foffi.
Link to paper: Soft Matter arXiv
Configurational entropy: Physical Review Letters arXiv
Granular: Nature Physics arXiv
Efficient event-driven simulations of hard spheres
Hard spheres are a long-time favorite model system of many soft matter scientists. Their simple interaction potential makes them both simple to simulate and readily realizable in the lab, but their dynamics and phase behavior is complex enough to allow for exploration of a wide variety of statistical physics phenomena, from crystallization to the glass transition. When simulating the dynamics of hard spheres, one small complication is that traditional molecular dynamics (MD) simulations do not work. Normally, we perform MD simulations by advancing time forward in small steps, calculating the forces on all particles, updating their velocities and positions, and moving on to the next time step. For hard spheres, this inevitably leads to overlaps, as the particles do not repel each other except at the exact moment of collision, which will be missed when stepping forward in fixed time steps. To address this, hard spheres are best simulated using event-driven simulations, where collision times are predicted between pairs of particles, and then handled in chronological order. Using a few optimization tricks, here I implented an efficient code for such simulations, which outperforms currently publicly available event-driven hard-sphere codes by up to approximately a factor of 10. This can lead to significant savings in terms of both computer time and energy.Link to paper: EPJE arXiv
Simulation code: GitHub
Autonomously revealing hidden local structures in supercooled liquids
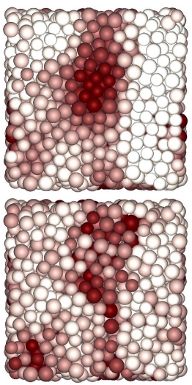 As shown in the work above, one way of predicting dynamics in glassy systems is to design order parameters that pick up on local structural variations that correlate with fast or slow-moving particles. However, this requires some clever guess-work. In this work, we show that an unsupervised machine learning algorithm can autonomously find the strongest structural variations in a glassy liquid, and that these variations show strong correlations with the dynamics of the individual particles. For hard-sphere mixtures, as studied in the work mentioned previously, the machine-learned order parameter even outperforms tetrahedrality. Our work shows that dynamical heterogeneities in glasses are directly linked to structural variation, and demonstrates that machine-learning methods can help us extract new insights from soft matter systems.
The figure shows a snapshot of a hard-sphere system with particles colored based on their structural variation (top, as detected by the unsupervised machine learning algorithm) and based on their mobility (bottom).
As shown in the work above, one way of predicting dynamics in glassy systems is to design order parameters that pick up on local structural variations that correlate with fast or slow-moving particles. However, this requires some clever guess-work. In this work, we show that an unsupervised machine learning algorithm can autonomously find the strongest structural variations in a glassy liquid, and that these variations show strong correlations with the dynamics of the individual particles. For hard-sphere mixtures, as studied in the work mentioned previously, the machine-learned order parameter even outperforms tetrahedrality. Our work shows that dynamical heterogeneities in glasses are directly linked to structural variation, and demonstrates that machine-learning methods can help us extract new insights from soft matter systems.
The figure shows a snapshot of a hard-sphere system with particles colored based on their structural variation (top, as detected by the unsupervised machine learning algorithm) and based on their mobility (bottom).
In collaboration with E. Boattini, S. Marín Aguilar, S. Mitra, G. Foffi, and L. Filion.
Link to paper: Nat. Commun. arXiv
Infinite-pressure phase diagram of binary mixtures of (non) additive hard disks
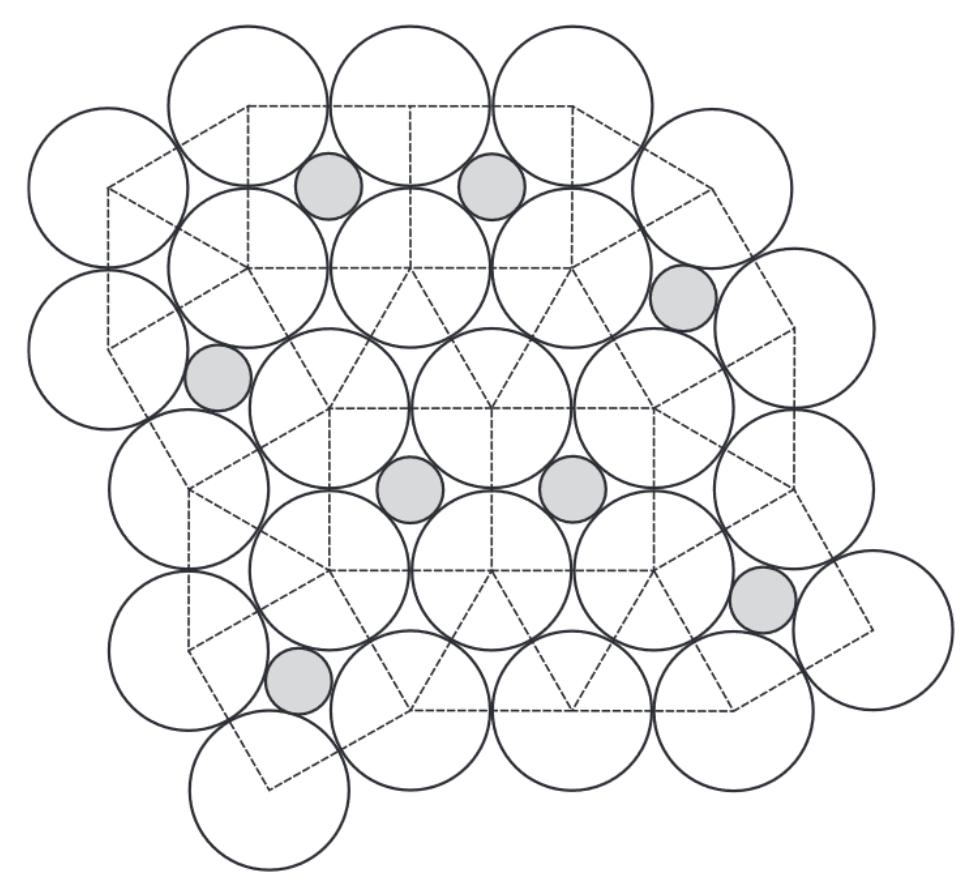 One of the most fascinating phenomena in soft matter science is the emergence of unexpected complex behavior from extremely simple model systems. In this work, we looked at simple systems of hard disks in a two-dimensional plane, and asked the question: what is the most efficient way to pack disks, such that we can fill as much of the plane as possible? If the disks are all the same size, the answer is a simple hexagonal crystal. However, just mixing two different sizes leads to a wealth of different crystal structures. Using Monte Carlo simulations, we attempted to locate the optimal packings for a range of mixtures of two sizes of disks, and -- depending on the size and number ratio -- found a wide variety of different crystal structures, including several that had not been previously considered for this system. We also considered the effect of non-additivity, where two disks are allowed to partially overlap if their sizes are different. This could occur, for example, if the particles we were studying were not actually flat disks, but two sizes of spheres confined to lie on a flat plane. Allowing non-additivity further expands the number of possible crystal phases. Perhaps most intriguing is the ability of these systems to form random tilings of squares and triangles that result in 12-fold quasicrystalline symmetry (see figure). Future work will also explore how these particles behave when not packed together perfectly, i.e. at finite pressures where thermal motion starts playing an important role.
One of the most fascinating phenomena in soft matter science is the emergence of unexpected complex behavior from extremely simple model systems. In this work, we looked at simple systems of hard disks in a two-dimensional plane, and asked the question: what is the most efficient way to pack disks, such that we can fill as much of the plane as possible? If the disks are all the same size, the answer is a simple hexagonal crystal. However, just mixing two different sizes leads to a wealth of different crystal structures. Using Monte Carlo simulations, we attempted to locate the optimal packings for a range of mixtures of two sizes of disks, and -- depending on the size and number ratio -- found a wide variety of different crystal structures, including several that had not been previously considered for this system. We also considered the effect of non-additivity, where two disks are allowed to partially overlap if their sizes are different. This could occur, for example, if the particles we were studying were not actually flat disks, but two sizes of spheres confined to lie on a flat plane. Allowing non-additivity further expands the number of possible crystal phases. Perhaps most intriguing is the ability of these systems to form random tilings of squares and triangles that result in 12-fold quasicrystalline symmetry (see figure). Future work will also explore how these particles behave when not packed together perfectly, i.e. at finite pressures where thermal motion starts playing an important role.
In collaboration with E. Fayen, A. Jagannathan, and G. Foffi.
Link to paper: J. Chem. Phys. arXiv
Topology of orientational defects in confined smectic liquid crystals
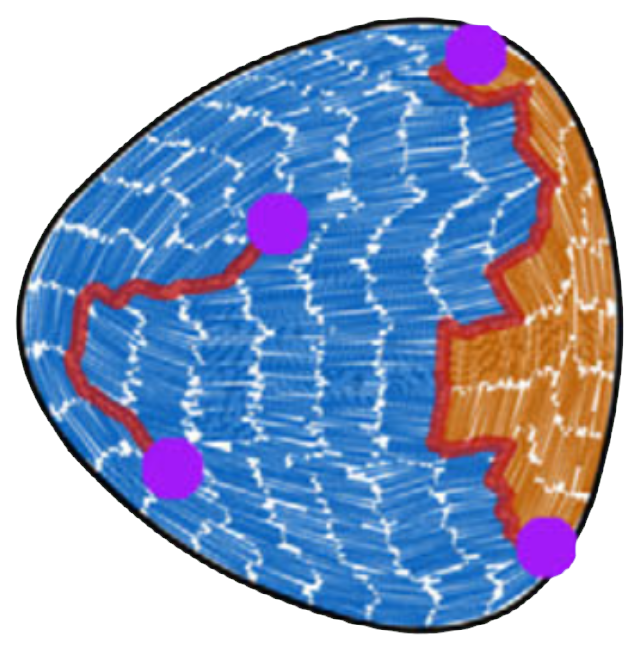 When rod-shaped particles are compressed to high densities they can form liquid crystals: layers of aligned particles that still lack the full ordering of a crystal. In a large two-dimensional system, where boundaries do not play a role, these layers will prefer to be straight, forming a relatively simple structure. However, when we confine these smectic liquid crystals in a set of external walls, this will lead to a variety of defects. In the case of hard rod-shaped particles and hard walls, the rods prefer to align with the wall, but this alignment will cause frustration, since not all walls are oriented along the same directions. Typically, the result is a set of distinct smectic domains, separated by grain boundaries and defects. In this work, we examined the patterns of grain boundaries in simulations of hard rods confined to a variety of different cavities. We classified the defect patterns using the concept of topological charge: since different smectic domains like to meet at angles of 0, 90, 180, or 270 degrees, grain boundaries always end or meet at points that can be interpreted as topological charges, with a charge of either 1/4 or -1/4. Our results also directly mapped to an experimental system of colloidal rods in confinement, where the same defect patterns occur.
When rod-shaped particles are compressed to high densities they can form liquid crystals: layers of aligned particles that still lack the full ordering of a crystal. In a large two-dimensional system, where boundaries do not play a role, these layers will prefer to be straight, forming a relatively simple structure. However, when we confine these smectic liquid crystals in a set of external walls, this will lead to a variety of defects. In the case of hard rod-shaped particles and hard walls, the rods prefer to align with the wall, but this alignment will cause frustration, since not all walls are oriented along the same directions. Typically, the result is a set of distinct smectic domains, separated by grain boundaries and defects. In this work, we examined the patterns of grain boundaries in simulations of hard rods confined to a variety of different cavities. We classified the defect patterns using the concept of topological charge: since different smectic domains like to meet at angles of 0, 90, 180, or 270 degrees, grain boundaries always end or meet at points that can be interpreted as topological charges, with a charge of either 1/4 or -1/4. Our results also directly mapped to an experimental system of colloidal rods in confinement, where the same defect patterns occur.
In collaboration with P. A. Monderkamp, R. Wittmann, L. B. G. Cortes, D. G. A. L. Aarts, F. Smallenburg, and H. Löwen.
Link to paper: Phys. Rev. Lett.
arXiv
Tetrahedrality dictates dynamics in hard spheres
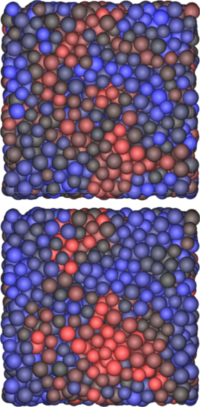 Within the same theme of linking local structure to glassy dynamics, here we explore the correlation between structure and glassy dynamics in a wide range of binary hard-sphere mixture with different size ratios, compositions, and packing fractions. Instead of focusing on icosahedra, we focus on the most fundamental local cluster possible in 3D: the tetrahedron. With its mechanical stability and efficient packing, the simple tetrahedron can be seen as the most fundamental local structure in a disordered fluid. Intriguingly, we find that the global diffusivity of a large range of hard-sphere mixtures can be predicted based only on the number of tetrahedral clusters per particle, with high tetrahedrality corresponding to slow dynamics. Moreover, local tetrahedrality provides an excellent predictor for future local dynamics, indicating that these structures indeed play a key role in slowing down rearrangements. As tetrahedra are also the key building block for many local structures previously linked to slow dynamics (including the icosahedron), this simple cluster may be the key to understanding glassy dynamics in a wide range of systems.
Within the same theme of linking local structure to glassy dynamics, here we explore the correlation between structure and glassy dynamics in a wide range of binary hard-sphere mixture with different size ratios, compositions, and packing fractions. Instead of focusing on icosahedra, we focus on the most fundamental local cluster possible in 3D: the tetrahedron. With its mechanical stability and efficient packing, the simple tetrahedron can be seen as the most fundamental local structure in a disordered fluid. Intriguingly, we find that the global diffusivity of a large range of hard-sphere mixtures can be predicted based only on the number of tetrahedral clusters per particle, with high tetrahedrality corresponding to slow dynamics. Moreover, local tetrahedrality provides an excellent predictor for future local dynamics, indicating that these structures indeed play a key role in slowing down rearrangements. As tetrahedra are also the key building block for many local structures previously linked to slow dynamics (including the icosahedron), this simple cluster may be the key to understanding glassy dynamics in a wide range of systems. The figure shows a snapshot of a glassy systems with particles colored either by tetrahedrality (top, red corresponds to low tetrahedrality) or mobility (bottom, red corresponds to high mobility).
In collaboration with S. Marín Aguilar, H. H. Wensink, and G. Foffi.
Link to paper: Phys. Rev. Lett., arXiv
Slowing down supercooled liquids by manipulating their local structure
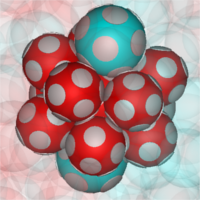 Recent research on a variety of glass formers has demonstrated that local structural ordering plays a key role in the dynamics of glassy liquids. In particular, the local packing of particles defines the cages which particles need to escape in order for the system to relax its structure. Here, we use this observation to tune the glassy dynamics of a model glass former using short-range directional (``patchy'') interactions. Starting from a dense binary-hard sphere mixture, we use computer simulations to explore the glassy dynamics of patchy particles with a wide range of geometries. We find that out of all geometries, particles with icosahedral symmetry are uniquely capable of facilitating dynamical arrest. In contrast, this slowdown is absent for the other investigated patch geometries. Hence, the slowest liquids are those where the particles enhance the number of icosahedral cages in the system. These cages are uniquely stable structures, which drastically impact the relaxation rate of the system. As icosahedral structures are also known to suppress the formation of long-ranged crystals, boosting their prevalence in a supercooled liquid is likely to lead to an excellent glass former. Our results highlight the special role of icosahedral caging in glassy liquids, and provide a way to control the dynamics of dense systems by selectively promoting specific local structural environments.
Recent research on a variety of glass formers has demonstrated that local structural ordering plays a key role in the dynamics of glassy liquids. In particular, the local packing of particles defines the cages which particles need to escape in order for the system to relax its structure. Here, we use this observation to tune the glassy dynamics of a model glass former using short-range directional (``patchy'') interactions. Starting from a dense binary-hard sphere mixture, we use computer simulations to explore the glassy dynamics of patchy particles with a wide range of geometries. We find that out of all geometries, particles with icosahedral symmetry are uniquely capable of facilitating dynamical arrest. In contrast, this slowdown is absent for the other investigated patch geometries. Hence, the slowest liquids are those where the particles enhance the number of icosahedral cages in the system. These cages are uniquely stable structures, which drastically impact the relaxation rate of the system. As icosahedral structures are also known to suppress the formation of long-ranged crystals, boosting their prevalence in a supercooled liquid is likely to lead to an excellent glass former. Our results highlight the special role of icosahedral caging in glassy liquids, and provide a way to control the dynamics of dense systems by selectively promoting specific local structural environments.
In collaboration with S. Marín Aguilar, H. H. Wensink, and G. Foffi.
Link to paper: Soft Matter
Erasing no-man's land by thermodynamically stabilizing the liquid-liquid transition in tetrahedral particles
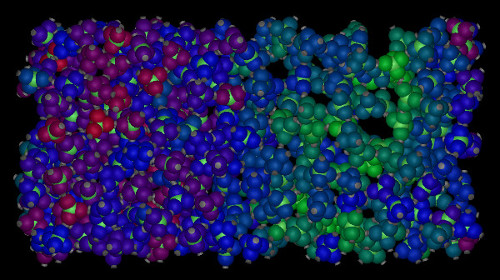 One of the more controversial topics in the study of water and other tetrahedrally coordinated liquids is the existence of a liquid-liquid phase transition. In this scenario, the liquid phase separates into a low-density and high-density liquid when cooled below the liquid-liquid critical temperature. Unfortunately, if such a transition exists, this critical temperature is far below the freezing temperature, and as a result, both experimental and computational tests of this hypothesis are plagued by rapid crystallization. In order to circumvent this problem, we designed a patchy particle model for tetrahedral liquids where the flexibility and length of the interparticle bonds can be independently controlled. Using extensive free-energy calculations, we show that a liquid-liquid phase transition is not only present in our model, but also that it can be completely stabilized with respect to crystallization by tuning the bond flexibility. As a result, the model provides a recipe for designing colloidal analogues of tetrahedral liquids that exhibit a liquid-liquid critical point.
One of the more controversial topics in the study of water and other tetrahedrally coordinated liquids is the existence of a liquid-liquid phase transition. In this scenario, the liquid phase separates into a low-density and high-density liquid when cooled below the liquid-liquid critical temperature. Unfortunately, if such a transition exists, this critical temperature is far below the freezing temperature, and as a result, both experimental and computational tests of this hypothesis are plagued by rapid crystallization. In order to circumvent this problem, we designed a patchy particle model for tetrahedral liquids where the flexibility and length of the interparticle bonds can be independently controlled. Using extensive free-energy calculations, we show that a liquid-liquid phase transition is not only present in our model, but also that it can be completely stabilized with respect to crystallization by tuning the bond flexibility. As a result, the model provides a recipe for designing colloidal analogues of tetrahedral liquids that exhibit a liquid-liquid critical point.
The picture shows a spontaneously formed liquid-liquid phase coexistence. The colors of the particles indicate the local density: red is high, green is low.
In collaboration with L. Filion and F. Sciortino.
Link to paper: Nat. Phys.
Commentary by Francis Starr: Nat. Phys.
Tuning the liquid-liquid transition by modulating the hydrogen bond angular flexibility in a model for water
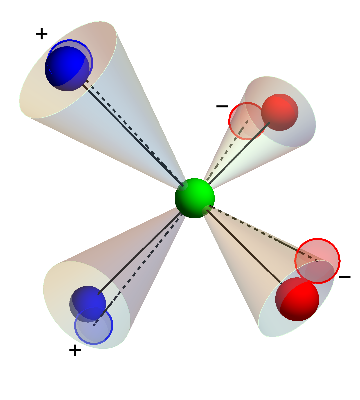 In a follow-up to the work above, we extended the concept of bond flexibility to a more realistic model for water known as the ST2 model. Although a liquid-liquid phase transition has been reported in ST2, it has been a matter of some debate whether this observation could be an artifact resulting from crystallization. In the ST2 model, each water molecule is considered as a rigid cluster of four point charges (two positive and two negative), around a central core. The molecules can form a tetrahedral network similar to those formed by the patchy particle systems we studied earlier. By allowing the charges within each molecule to fluctuate, we can increase the bond flexibility of this model. We show that, as in the case of the patchy-particle model, increasing the flexibility results in a full stabilization of the liquid-liquid transition with respect to the low-density (diamond) crystal structure, such that nucleation of this structure is no longer a concern. Our results provide additional evidence for the presence of a true liquid-liquid critical point in ST2, and emphasize again that bond flexibility is a key parameter for determining the existence of a secondary liquid phase in tetrahedral liquids.
In a follow-up to the work above, we extended the concept of bond flexibility to a more realistic model for water known as the ST2 model. Although a liquid-liquid phase transition has been reported in ST2, it has been a matter of some debate whether this observation could be an artifact resulting from crystallization. In the ST2 model, each water molecule is considered as a rigid cluster of four point charges (two positive and two negative), around a central core. The molecules can form a tetrahedral network similar to those formed by the patchy particle systems we studied earlier. By allowing the charges within each molecule to fluctuate, we can increase the bond flexibility of this model. We show that, as in the case of the patchy-particle model, increasing the flexibility results in a full stabilization of the liquid-liquid transition with respect to the low-density (diamond) crystal structure, such that nucleation of this structure is no longer a concern. Our results provide additional evidence for the presence of a true liquid-liquid critical point in ST2, and emphasize again that bond flexibility is a key parameter for determining the existence of a secondary liquid phase in tetrahedral liquids.
The picture shows a schematic representation of the ST2 model with added flexibility.
In collaboration with F. Sciortino.
Link to paper: Phys. Rev. Lett., arXiv
Liquids more stable than crystals in particles with limited valence and flexible bonds
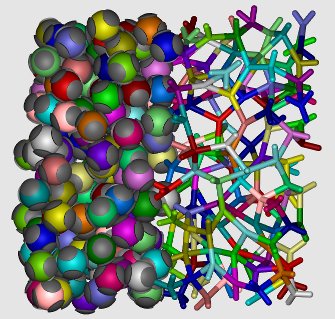 Patchy particles with four tetrahedrally arranged patches are known to form a low-density diamond crystal phase at low temperatures, but this phase becomes less stable as the size of the patches (or bond flexibility) increases. We investigated the effect of patch width on the phase behavior of patchy particles modeled via the Kern-Frenkel model, with the additional limitation that each patch can form at most a single bond. This limitation allows us to examine particles with highly flexible bonds that nevertheless maintain a limited valence. In these systems, the low-density crystal phase vanishes from the phase diagram, and is replaced by a region where the liquid phase is stable even in the low-temperature limit. This almost fully bonded liquid is stabilized by the configurational entropy associated with the number of ways the network can be bonded. Additionally, we show that the diffusion in the liquid is dominated by the hopping of broken bonds.
Patchy particles with four tetrahedrally arranged patches are known to form a low-density diamond crystal phase at low temperatures, but this phase becomes less stable as the size of the patches (or bond flexibility) increases. We investigated the effect of patch width on the phase behavior of patchy particles modeled via the Kern-Frenkel model, with the additional limitation that each patch can form at most a single bond. This limitation allows us to examine particles with highly flexible bonds that nevertheless maintain a limited valence. In these systems, the low-density crystal phase vanishes from the phase diagram, and is replaced by a region where the liquid phase is stable even in the low-temperature limit. This almost fully bonded liquid is stabilized by the configurational entropy associated with the number of ways the network can be bonded. Additionally, we show that the diffusion in the liquid is dominated by the hopping of broken bonds.
The picture shows the particles (left) and bonds (right, connecting the centers of bonded particles) in a fully bonded disordered network.
In collaboration with F. Sciortino.
Link to paper: Nat. Phys., arXiv
Commentary by Jeppe Dyre: Nat. Phys.
Patchy particle model for vitrimers
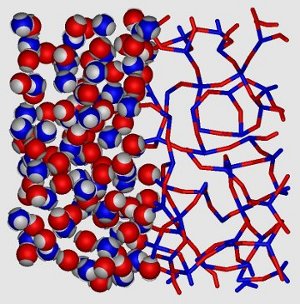 Vitrimers are a recently invented class of polymers with highly useful material properties. They are covalently bonded networks, consisting of (typically) two types of monomers, each with a limited functionality (or valence). The bonds can rearrange, and thus relax the network topology, via catalyst-aided bond exchange reactions. Since only bonds between monomers of different species are allowed, and the covalent bonds are too strong to break, the total number of bonds in the system is essentially fixed by the composition. Using a variation on our wide-patch Kern-Frenkel model (see above), we demonstrate a patchy-particle model for vitrimers that mimicks the unique bond-switching mechanic of vitrimers. We calculate the phase diagram of the model using both simulations and a simple, parameter-free thermodynamic perturbation theory, and show that vitrimers are expected to phase separate at low densities into a highly bonded network phase and a dilute gas phase. Additionally, we investigate the viscosity in our model system, and show that the model exhibits the same strong (silica-like) glass-forming behavior that is observed in vitrimers.
Vitrimers are a recently invented class of polymers with highly useful material properties. They are covalently bonded networks, consisting of (typically) two types of monomers, each with a limited functionality (or valence). The bonds can rearrange, and thus relax the network topology, via catalyst-aided bond exchange reactions. Since only bonds between monomers of different species are allowed, and the covalent bonds are too strong to break, the total number of bonds in the system is essentially fixed by the composition. Using a variation on our wide-patch Kern-Frenkel model (see above), we demonstrate a patchy-particle model for vitrimers that mimicks the unique bond-switching mechanic of vitrimers. We calculate the phase diagram of the model using both simulations and a simple, parameter-free thermodynamic perturbation theory, and show that vitrimers are expected to phase separate at low densities into a highly bonded network phase and a dilute gas phase. Additionally, we investigate the viscosity in our model system, and show that the model exhibits the same strong (silica-like) glass-forming behavior that is observed in vitrimers.
The picture shows the particles (left) and bonds (right) in part of a vitrimer network. The different colors indicate different monomer species: 4-patch (blue) and 2-patch (red) particles.
In collaboration with L. Leibler and F. Sciortino.
Link to paper: Phys. Rev. Lett.
Close packing of rods on spherical surfaces
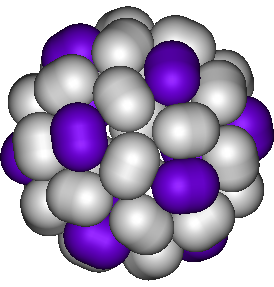 The best way to pack spheres or rods densely in a flat plane is on a simple periodic lattice. However, the best packing of particles on a spherical surface is much less clear, and strongly dependent on the ratios between the rod length, the rod diameter, and the radius of the spherical surface. Using numerical optimization techniques, we explored the best packed structures for short rods on spherical surfaces, and found a rich variety of cluster symmetries. Intriguingly, very short rods both come closer to their maximum packing and form fewer defects than both spheres and longer rods, assuming clusters of similar size. Our results could guide the design of colloidosomes -- hollow shells of colloidal particles self-assembled on the surface of e.g. emulsion droplets -- with new symmetries and pore size distributions.
The best way to pack spheres or rods densely in a flat plane is on a simple periodic lattice. However, the best packing of particles on a spherical surface is much less clear, and strongly dependent on the ratios between the rod length, the rod diameter, and the radius of the spherical surface. Using numerical optimization techniques, we explored the best packed structures for short rods on spherical surfaces, and found a rich variety of cluster symmetries. Intriguingly, very short rods both come closer to their maximum packing and form fewer defects than both spheres and longer rods, assuming clusters of similar size. Our results could guide the design of colloidosomes -- hollow shells of colloidal particles self-assembled on the surface of e.g. emulsion droplets -- with new symmetries and pore size distributions.
The picture shows a highly symmetric close-packed cluster of 42 rods.
In collaboration with H. Löwen
Link to paper: arXiv
Vacancy-stabilized crystalline order in hard cubes
 At first glance, hard cubes seem to be a simple system, but its (simple cubic) crystalline phase shows some surprising properties. Using free energy calculations, we showed that close to the melting point, the equilibrium crystal phase shows a surprisingly high concentration of vacancies: while the particles are on average placed on a crystal lattice, there can be up to 6% fewer particles than lattice sites in the system. Moreover, the vacancies are delocalized; they are spread out over multiple lattice sites, increasing the freedom of movement for several nearby particles. In event-driven molecular dynamics simulations, these vacancies can be shown to be highly mobile, leading to a highly diffusive crystal phase. The picture is a snapshot of a typical crystalline configuration, where the vacancies and the particles which surround the vacancy have been highlighted (yellow).
At first glance, hard cubes seem to be a simple system, but its (simple cubic) crystalline phase shows some surprising properties. Using free energy calculations, we showed that close to the melting point, the equilibrium crystal phase shows a surprisingly high concentration of vacancies: while the particles are on average placed on a crystal lattice, there can be up to 6% fewer particles than lattice sites in the system. Moreover, the vacancies are delocalized; they are spread out over multiple lattice sites, increasing the freedom of movement for several nearby particles. In event-driven molecular dynamics simulations, these vacancies can be shown to be highly mobile, leading to a highly diffusive crystal phase. The picture is a snapshot of a typical crystalline configuration, where the vacancies and the particles which surround the vacancy have been highlighted (yellow).
In collaboration with L. Filion, M. Marechal, and M. Dijkstra.
Link to paper: PNAS, arXiv
Commentary by Daan Frenkel: PNAS
Highlighted in the Journal Club for Condensed Matter Physics: 1 2
Phase diagram of colloidal spheres in a biaxial electric or magnetic field
 Colloidal particles with a dielectric constant mismatch with the surrounding solvent in an external biaxial magnetic or electric field experience an ``inverted'' dipolar interaction, where particles attract in the plane of the external field, and repel in the direction perpendicular to it, resulting in sheet-like structures. We determine the phase behavior of hard spheres in such a field, using Helmholtz free energy calculations and Monte Carlo simulations, both with and without an additional screened-charge repulsion. Without charges, the phase diagram shows a gas-liquid transition, a hexagonal ABC stacked crystal phase, and a stretched hexagonal-close-packed crystal. The phase diagram for charged spheres is very similar, but displays an additional layered-fluid phase. We compare our results with recent experimental observations.
Colloidal particles with a dielectric constant mismatch with the surrounding solvent in an external biaxial magnetic or electric field experience an ``inverted'' dipolar interaction, where particles attract in the plane of the external field, and repel in the direction perpendicular to it, resulting in sheet-like structures. We determine the phase behavior of hard spheres in such a field, using Helmholtz free energy calculations and Monte Carlo simulations, both with and without an additional screened-charge repulsion. Without charges, the phase diagram shows a gas-liquid transition, a hexagonal ABC stacked crystal phase, and a stretched hexagonal-close-packed crystal. The phase diagram for charged spheres is very similar, but displays an additional layered-fluid phase. We compare our results with recent experimental observations. The picture shows different phases in the charged system: (a) gas, (b) liquid (c) layered fluid, (d) crystal.
In collaboration with M. Dijkstra.
Link to paper: J. Chem. Phys.